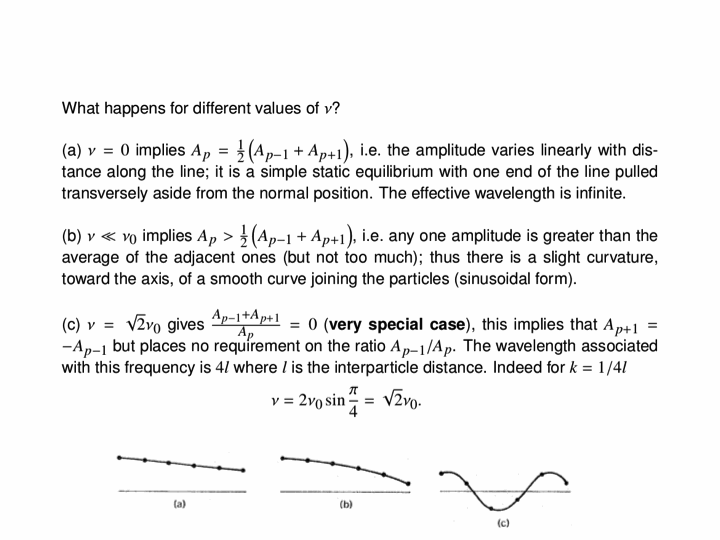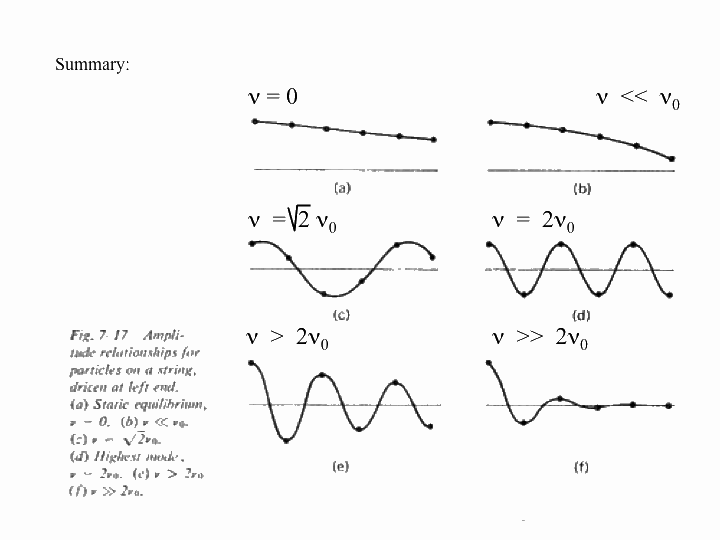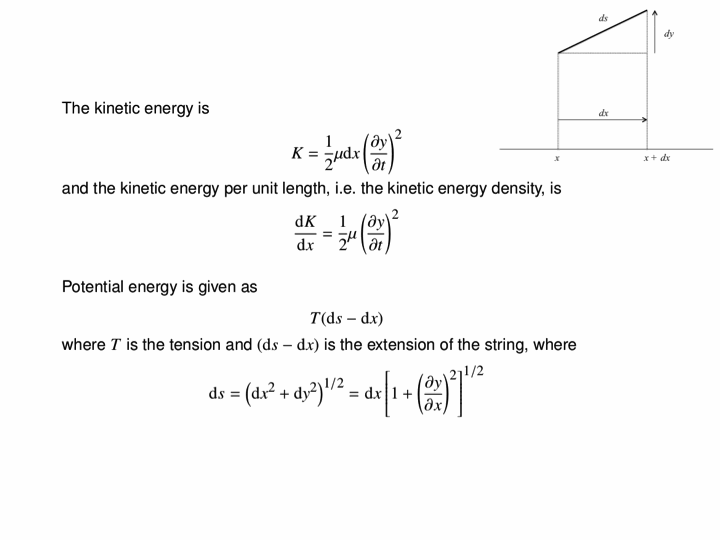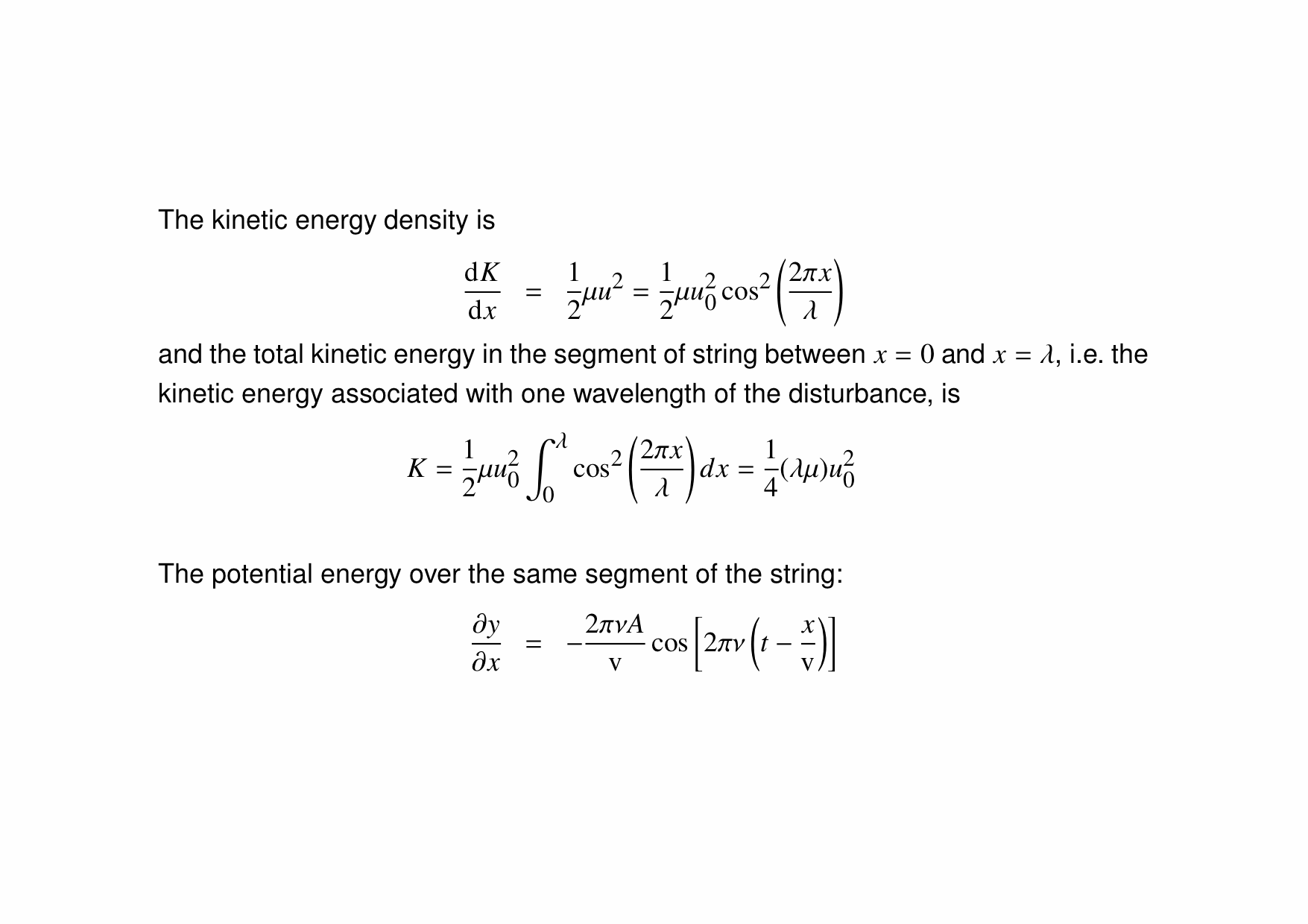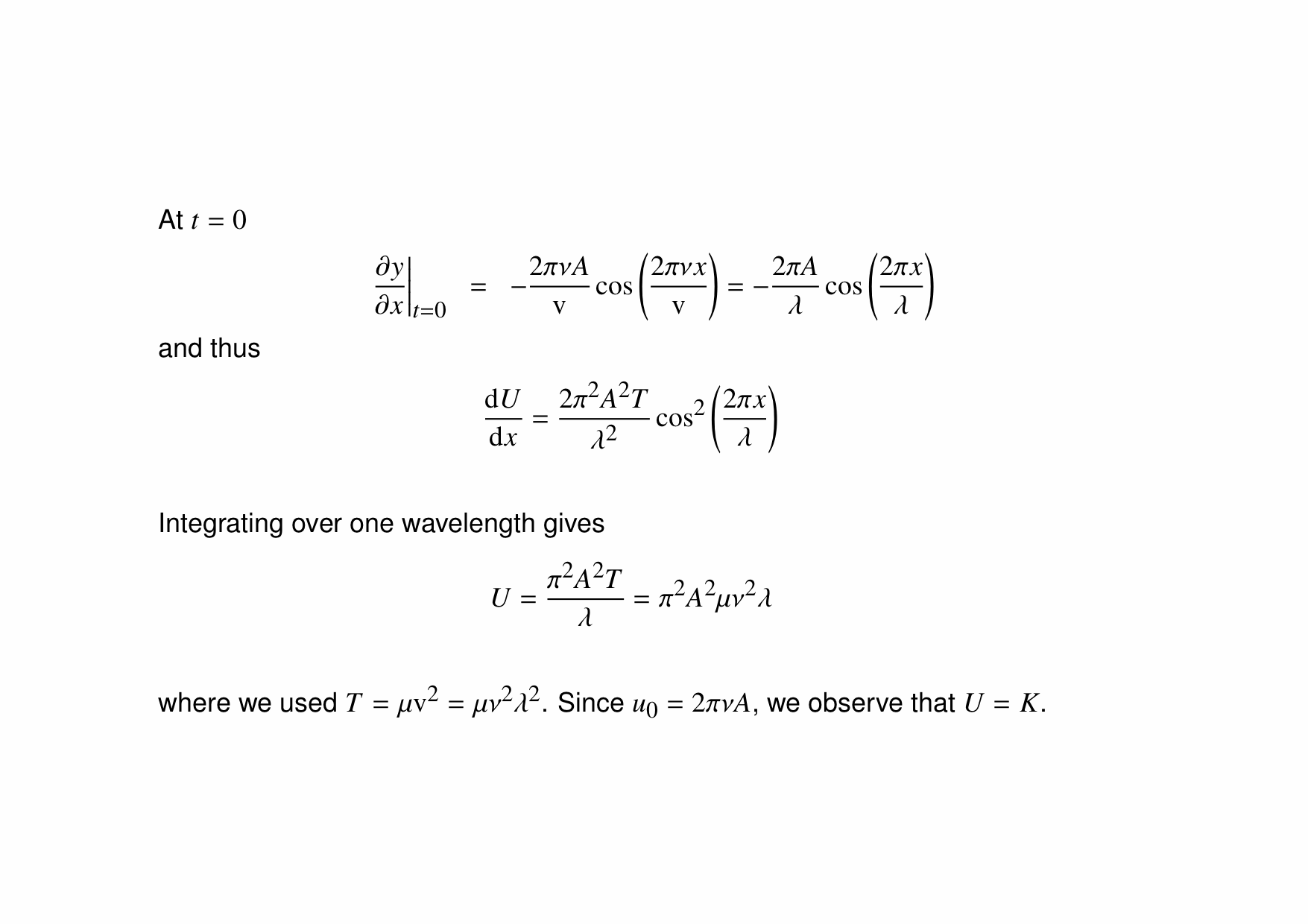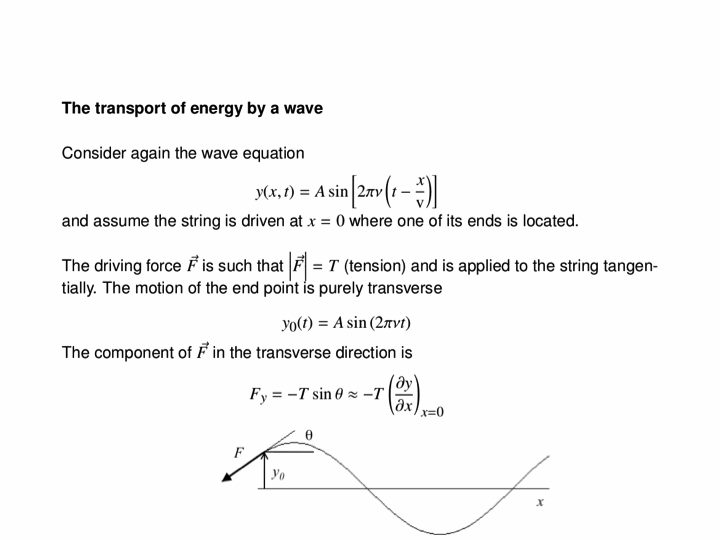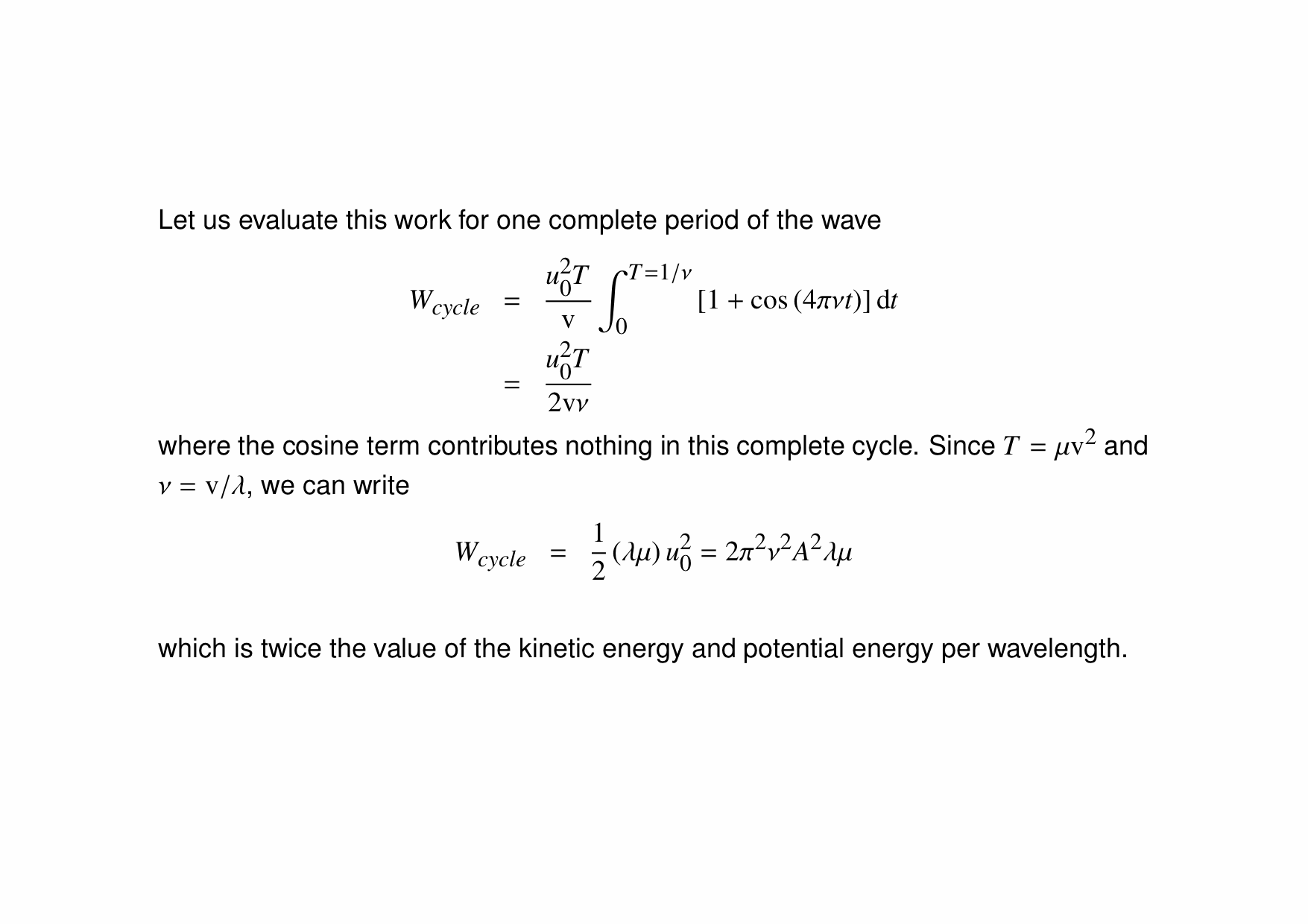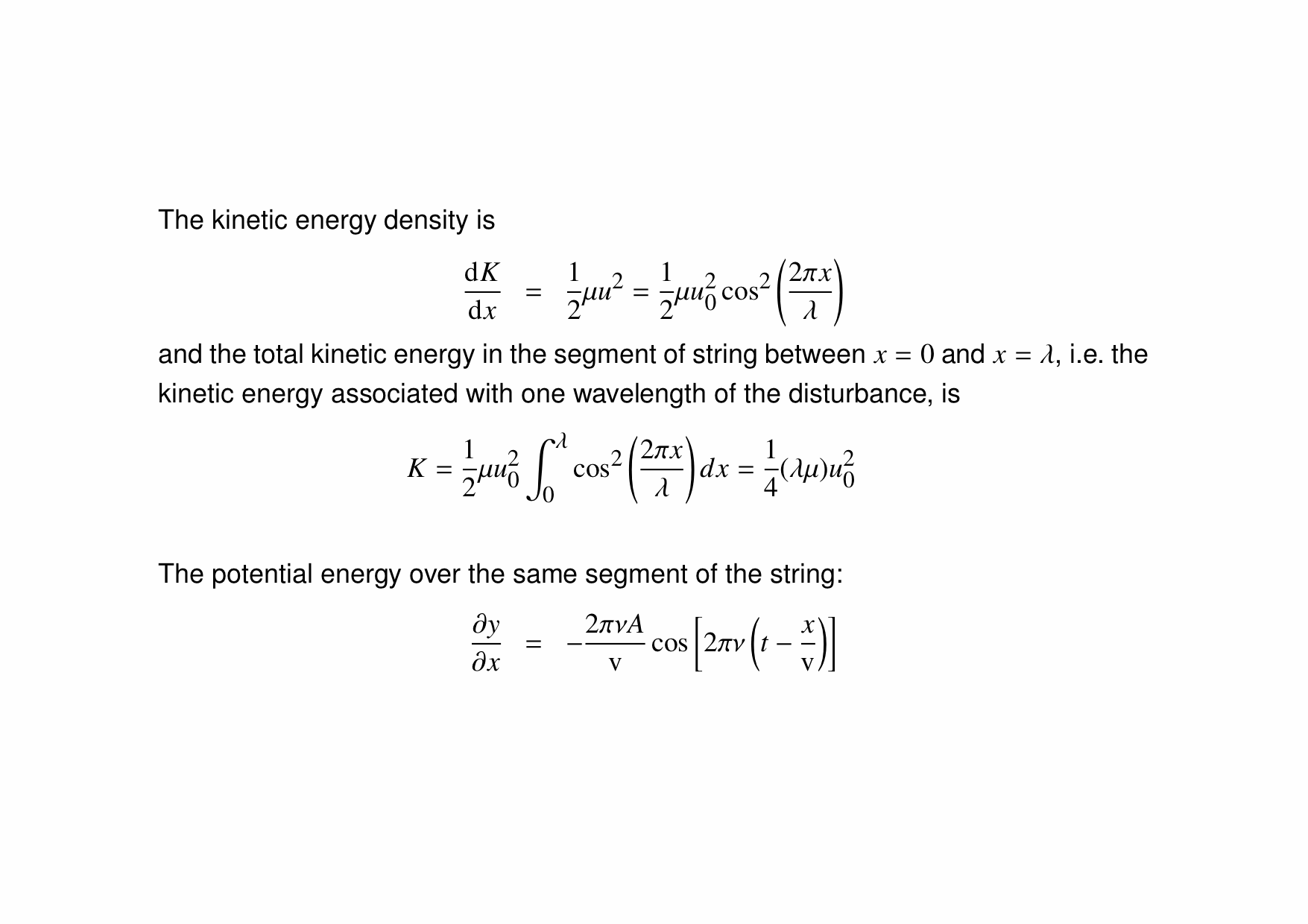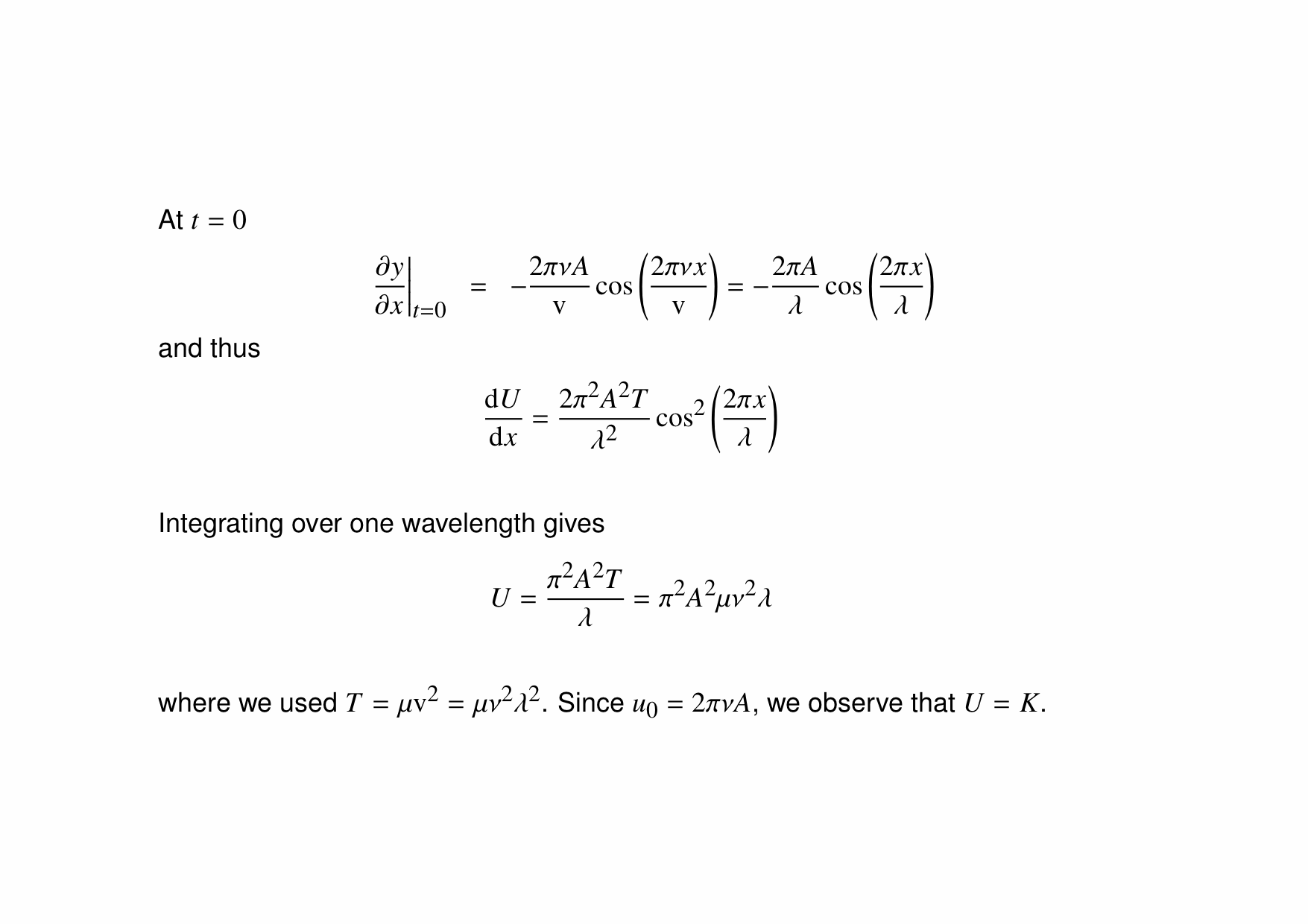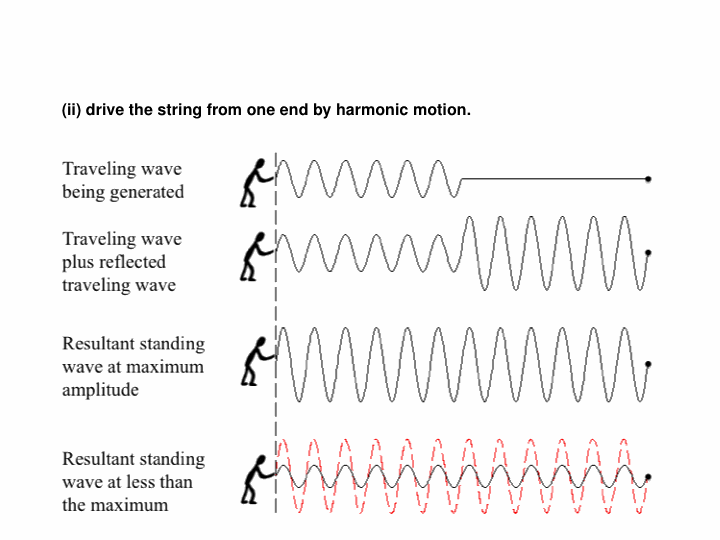
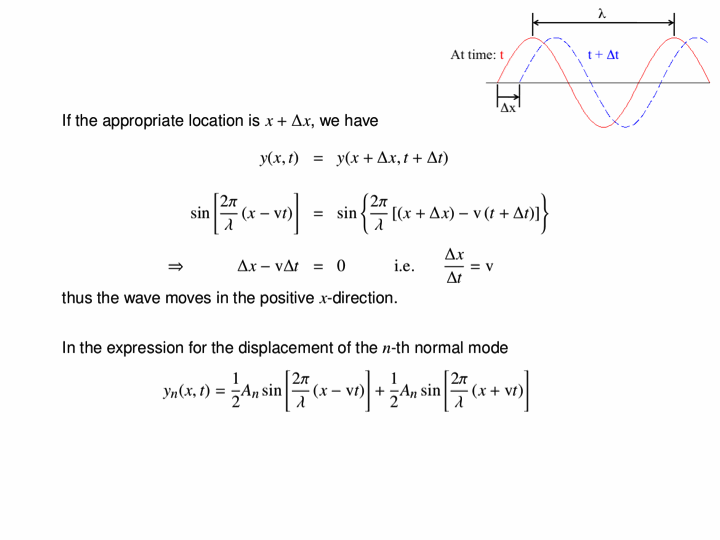
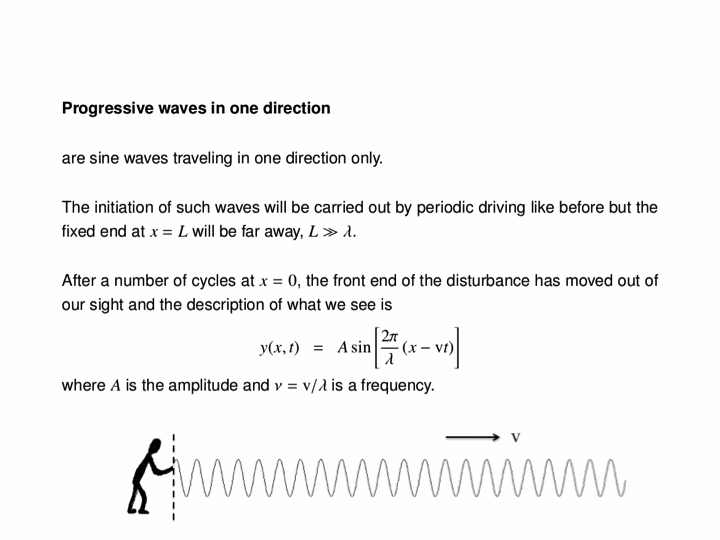
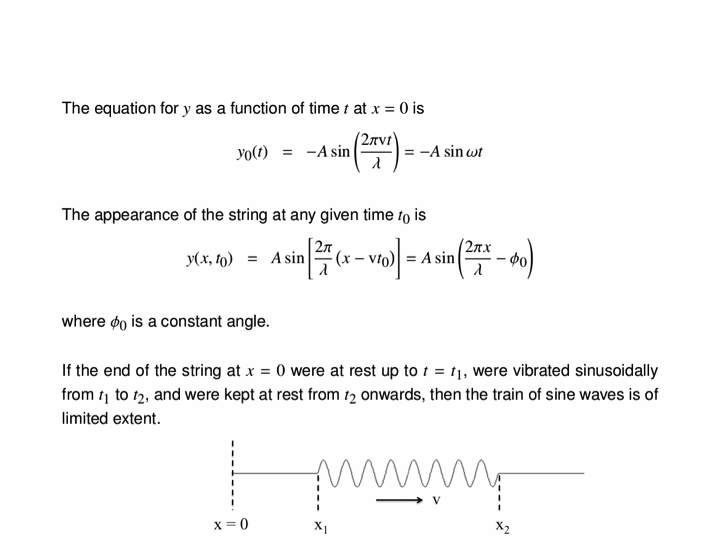
In this animation, we see how driving a string harmonically produces a travelling wave. The left end of the string is moved up and down, and this produces a wave travelling to the right along the (approximately) infinitely-long string.
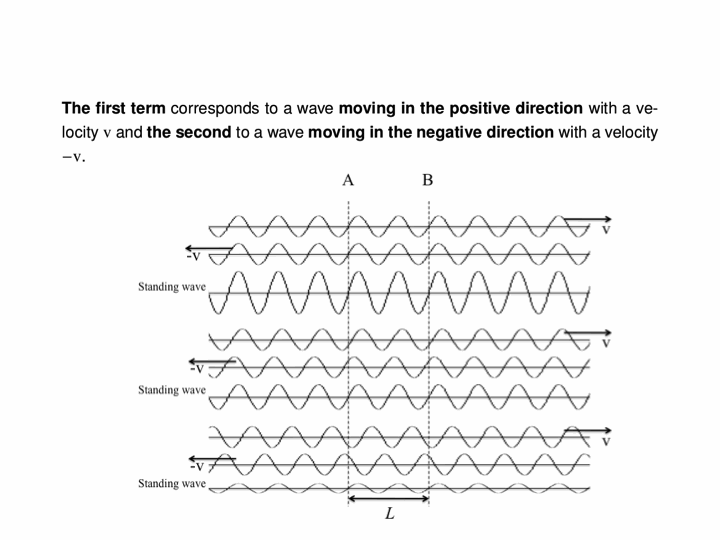
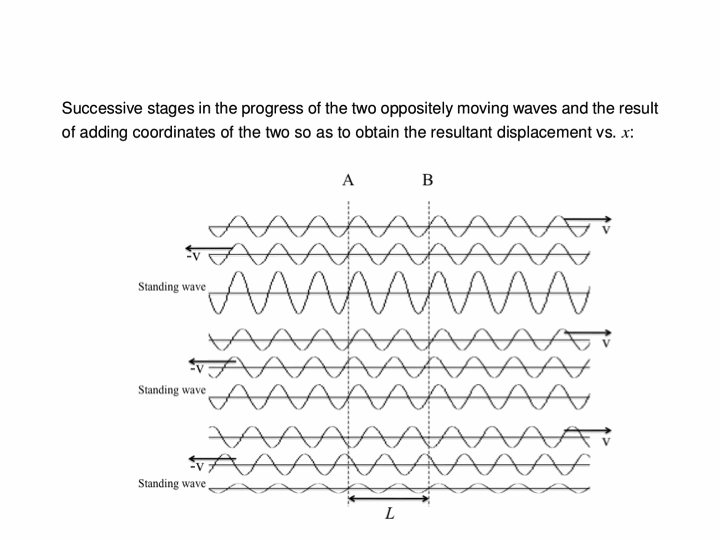
Here we see the superposition of two waves which are identical in frequency, amplitude and speed but travel in opposite directions. The top two waves travel, respectively, to the right and to the left, but their sum (the bottom wave) does not travel at all. Its amplitude oscillates, but the peaks and troughs occur at the same places at all times.


































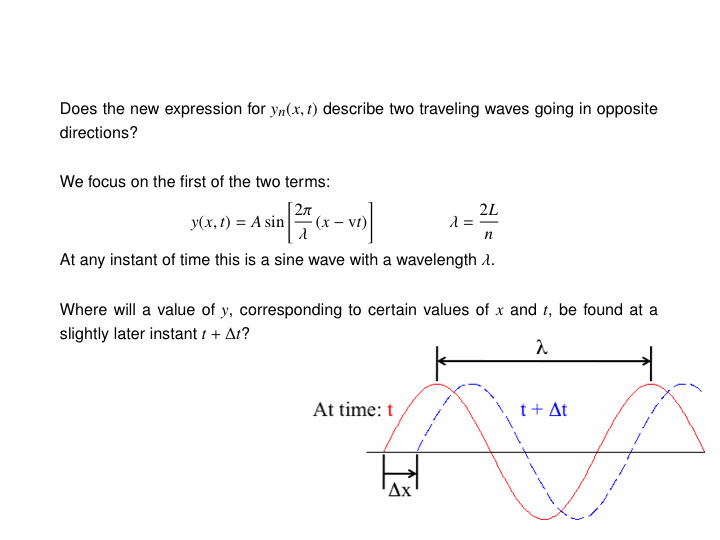
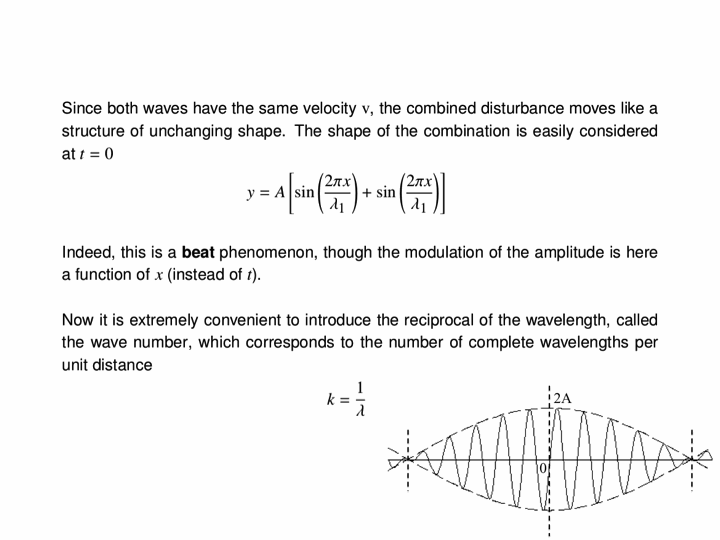
Here are two examples of wave pulses. The first is a simple sine wave, but one of finite length (two wavelengths, to be exact): The second is a Gaussian pulse, characterised by its amplitude and its width:










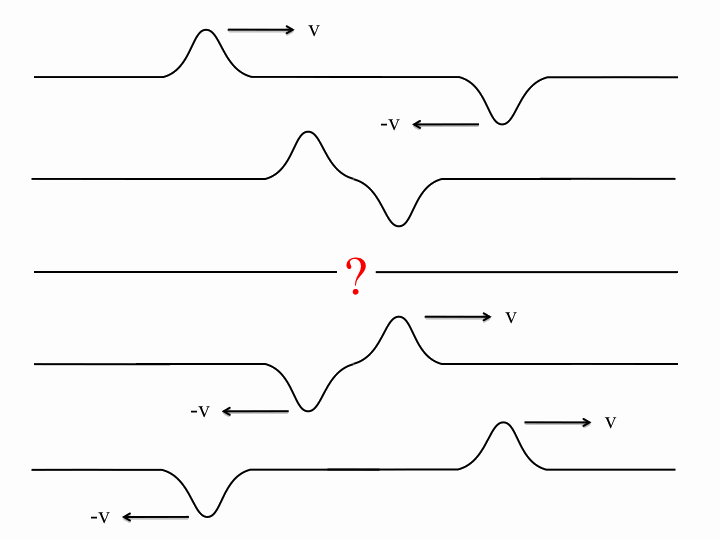
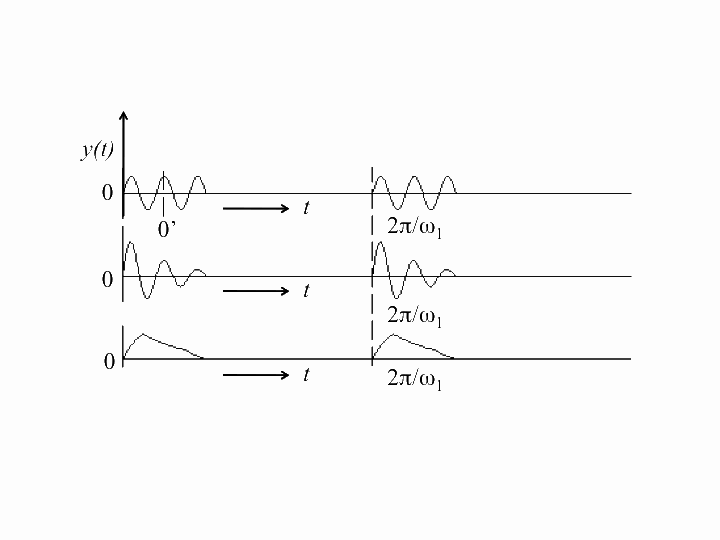
Here are two Gaussian pulses of the same speed and width, but with opposite amplitudes and travelling in opposite directions. You can see explicitly that there is a point in time at which they completely cancel each other out and the string is perfectly straight. However, because the string is still moving transversally at this point, the two pulses reemerge and eventually travel along as if nothing had ever happened.











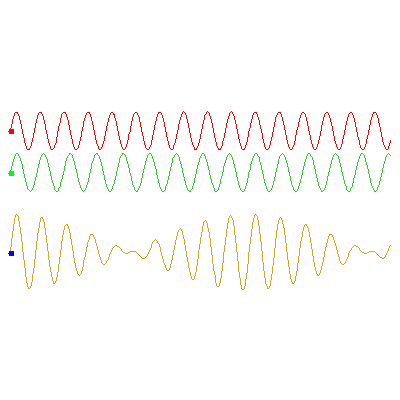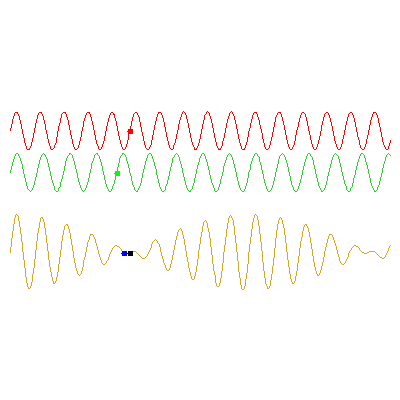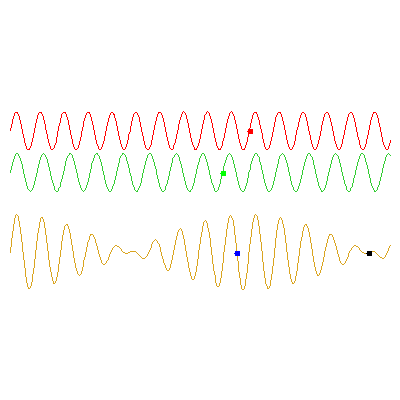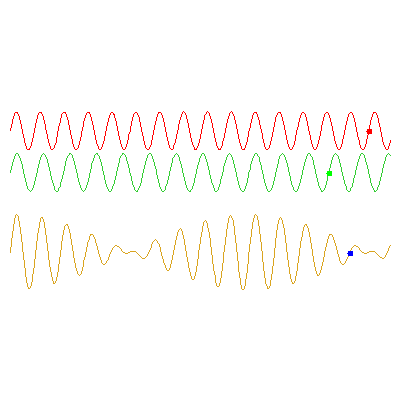
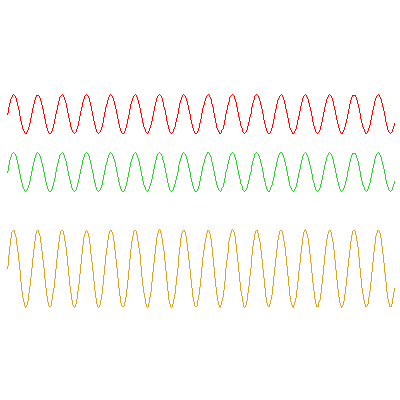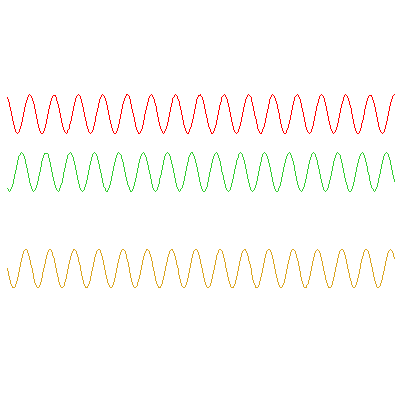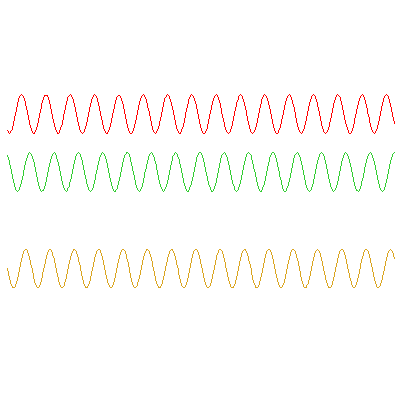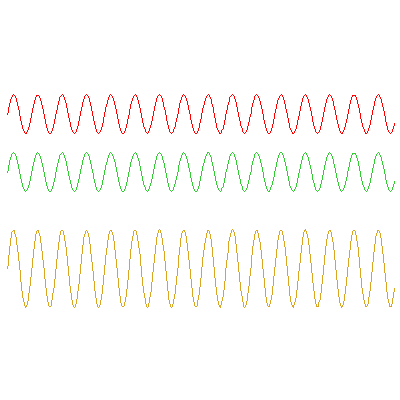
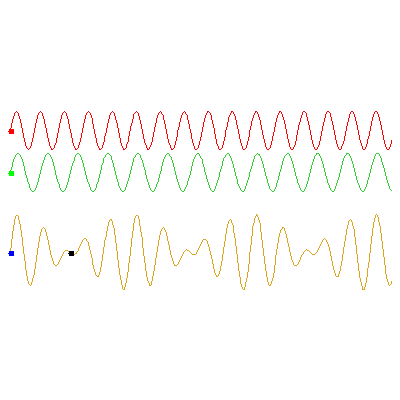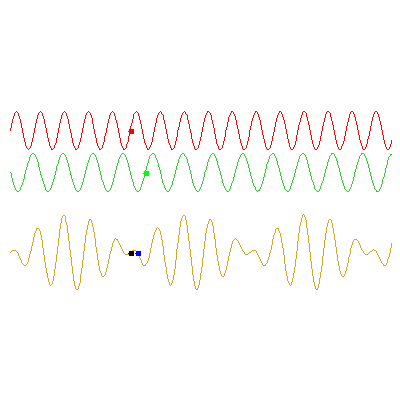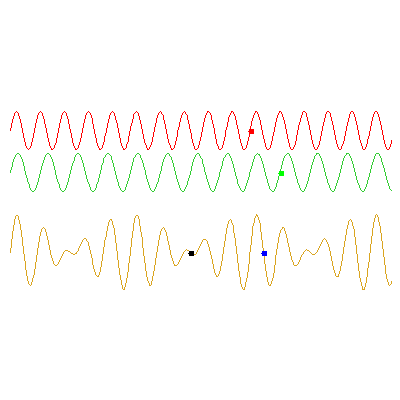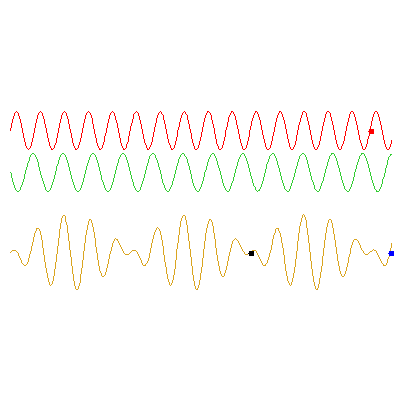
The below animations illustrate the difference between phase and group velocities; the top two waves travel with speeds indicated by the red and green dots, and the phase and group velocities of their sum (the bottom wave) can be seen from the movement of the blue and black dots respectively.

In the first example, the red wave has frequency $\omega_1=3\pi/5 \,\mathrm{rad}\cdot\mathrm{s}^{-1}$ and the green has $\omega_2=0.9\omega_1$. The speed of the green wave is 9/8 times the speed of the red; the phase velocity of the orange wave is the average of these (17/16 times the red wave's speed), and the group velocity -- the speed at which the envelope travels -- is half of the red wave's speed: In this second example, the red wave is the same, but now the green has frequency $\omega_2=0.8\omega_1$ and travels at 8/9 times the speed of the red. The phase velocity of the orange wave is now 17/18 times the red wave's speed its group velocity is twice the red wave's speed: